Výpočet vytvořený v minulém příspěvku NSD pro úplné začátečníky už funguje, takže přichází první myšlenka, zda by to šlo vylepšit.
Tento algoritmus je natolik neefektivní, že možností je spousta. Pro inspiraci uvedu tři nejjednodušší.
Ukončit odečítaní, když jedno z čísel je jedna
Jakmile je jedno z čísel 1, je zřejmé, že algoritmus skončí až se od druhého čísla odečte 1 tolikrát, že zbyde taky 1. Takže když jedno číslo je jedna, výsledek nemůže být jiný než 1. Proto můžeme skončit dřív a vypsat jako výsledek 1. Řešením je přidat za odečítání nový if, který musí být stále součást cyklu while, aby se provedl vždy. Pokud je a nebo b rovné 1, tak použijeme příkaz break, který ukončí cyklus. Před break je potřeba nastavit obě proměnné na 1, aby to odpovídalo stavu jakoby cyklus korektně skončil.
Zadání čísel vstupem od uživatele
Aby proměnné a a b nebyly zadány natvrdo, je možné o zadání požádat uživatele. Vstup hodnoty z klávesnice se liší podle verze Python, kterou použijete. Moje ukázka je z Python 3.x, v případě Python 2.x by stačila jen funkce input(), která se ale z bezpečnostních důvodů nedoporučuje používat.
Funkce input() vypíše text zadaný jako parametr na obrazovku a načte řetezec z klávesnice po stisk klávesy Enter. Řetězec je předán do funkce int(), která to převede na celé číslo, pokud řetězec odpovídá celému číslu. Pokud obsahuje neplatný znak, načtení skončí výjimkou. Zpracování výjimek se budeme věnovat v dalším pokračování.
Kontrola před začátkem výpočtu
Použitý algoritmus má zásadní problém, že nikdy neskončí pokud by jedno ze vstupních čísel bylo nula, nebo by se úplně zbláznil, pokud by některé číslo bylo záporné. Pak by místo odečítání přičítal a program by běžel donekonečna. Proto je na začátek přidán test, který zkontroluje vstupní čísla a pokud je kterékoliv menší než 1, vypíše pomocí print informaci o chybě a skončí.
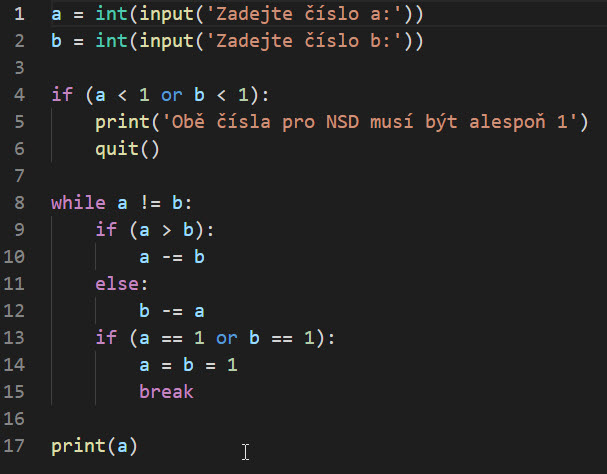
Upravené jsou řádky 1 a 2, přidané jsou řádky 4 až 6 a 13 až 15.
Tento jednoduchý příklad umožňuje lehce demonstrovat, že je potřeba přemýšlet o algoritmu a hledat zda nenastane situace, kdy lze jednoznačně určit výsledek a je zbytečné dál počítat. A že je potřeba vždy vyhodnotit, zda neexistují vstupní data která by znamenala nefunkčnost algoritmu a použití těchto dat je nutno zabránit.