Výpočet Největšího společného dělitele (NSD) v oboru kladných celých čísel je ideální jako startovací zadání pro programování. Student by už měl mít povědomí o tom co to je, v matematice by to už měl umět používat a pokud umí zlomky, měl by tušit, že se to hodí při výpočtu základního tvaru zlomku.
Určit NSD jde několika cestami. Od rozkladu na prvočinitele a pak hledání stejných prvočísel v obou rozkladech po Euklidův algoritmus, který využívá dělení se zbytkem.
Můj oblíbenec je algoritmus velice jednoduchý, ale co se výpočtu týče velice neefektivní. To nás ale při prvním programu nemusí trápit, máme pak alespoň co vylepšovat.
Popis algoritmu
- Připravte si čísla a, b. Obě musí být větší než nula.
- Pokud a je různé od b, pokračujte krokem 3. Pokud jsou stejné, je hotovo, NSD se rovná daným číslům a dál nepokračujeme.
- Zjistím které z čísel a a b je větší. Do většího přiřadím rozdíl mezi menším a větším. A pak opět vykonám krok 2.
Tak například pokud by na začátku bylo a = 24 a b = 16.
a a b nejsou stejné, a je větší, takže do a přiřadím 24 – 16 = 8. Po prvním vykonání algoritmu mám a = 8 a b = 16.
Stále nejsou a i b stejné, takže tentokrát od b (je větší) odečtu a (16 – 8 = 8). Takže do b přiřadím 8.
Teď je v a i b číslo 8, takže mohu skončit, dál není důvod pokračovat, podmínka nerovnosti není splněna
Popis řešení
Na začátku je nutno nastavit proměnné a i b. Dle jazyka doporučuji v první fázi nastavit čísla natvrdo, neočekávat vstup z klávesnice.
Dalším krokem je použití cyklu while. Podmínku jasně vyhodnocujeme dřív než něco budeme dělat. Testovat budeme nerovnost mezi proměnnými a a b.
Uvnitř cyklu while potřebuji if, který vyhodnotí která z proměnných je větší a podle výsledku provedeme výpočet rozdílu a přiřazení.
Vzorový příklad řešení – jazyk Python
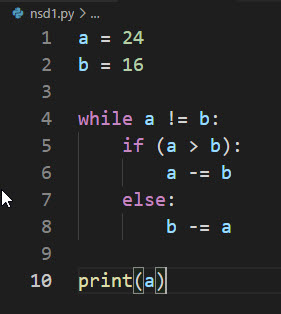
Na tomto úplně jednoduchém příkladu studenti vidí jak použití cyklu, tak rozhodovací if i zápis operace s přiřazením. Zda algoritmus funguje si můžou lehce zkusit. A těm šikovnějším můžete zadat otázku, zda dovedou vysvětlit, proč ten algoritmus funguje.